Covering an arbitary area with Circles of equal radius

The problem
The Idea
The Solution
Demo
Resource

Maps help us to visualize different aspects of our work. We use them when we want to get information about the place when we order a taxi and in many other cases.

Recently, I received a task to calculate a centers position of the areas with the equal area that is evenly distributed inside picked by user area (inside some polygon).

We can simplify the task by saying that we should “eventually fill (or cover) the polygon with smaller shapes of equal size (circles, for example)” on map.

The problem

Such an approach can help a lot for a different kind of task, and I believe there are a lot of existing algorithms that may help us to do this. Below, I tried to represent my approach to doing this.

k-center clustering one of algorithm. On SO there is also a few related to this algorithm questions exist, like this one

If u need to evenly distribute something over a certain area, or create a kind of protective shield on some area - this algorithm - is exactly what are u looking for.

To cover the space with regular polygon, only 3 tessellations of 2D space exists - use squares, triangles, or hexagons. In case if we would like to use other shapes, like a circle, overlapping will be present.

If u review all 3 approaches, then, basically, u can see that all of them consist of triangles - 1 or more

If we talking about circles as a covering shape, then hexagons are the ideal solution - it represents a circle that a bit triangulated.

The idea - is to tessellate hexagons and then circumscribe a circle to every polygon. Hexagon as a basic shape reduces the amount of overlapping.

This method is known as Hexagonal tiling. If we talk about volume - Close-packing of equal spheres may be helpful

The Idea

I was thinking about a possible way of calculating centers of covering shapes and how to cover the shape with hexagons. Then, found pretty similar description of the idea by baskax as I was thinking about:

1) Define the polygon area to be covered

2) Define the parameters of the shape to be used as covering shape

3) Cover the full area with a hexagon (or triangles or squares)

4) Determine what centers of shapes are inside of your initial polygon and select them

5) Replace shape from p3. to selected shape

As always, one picture is better that 1000 words:

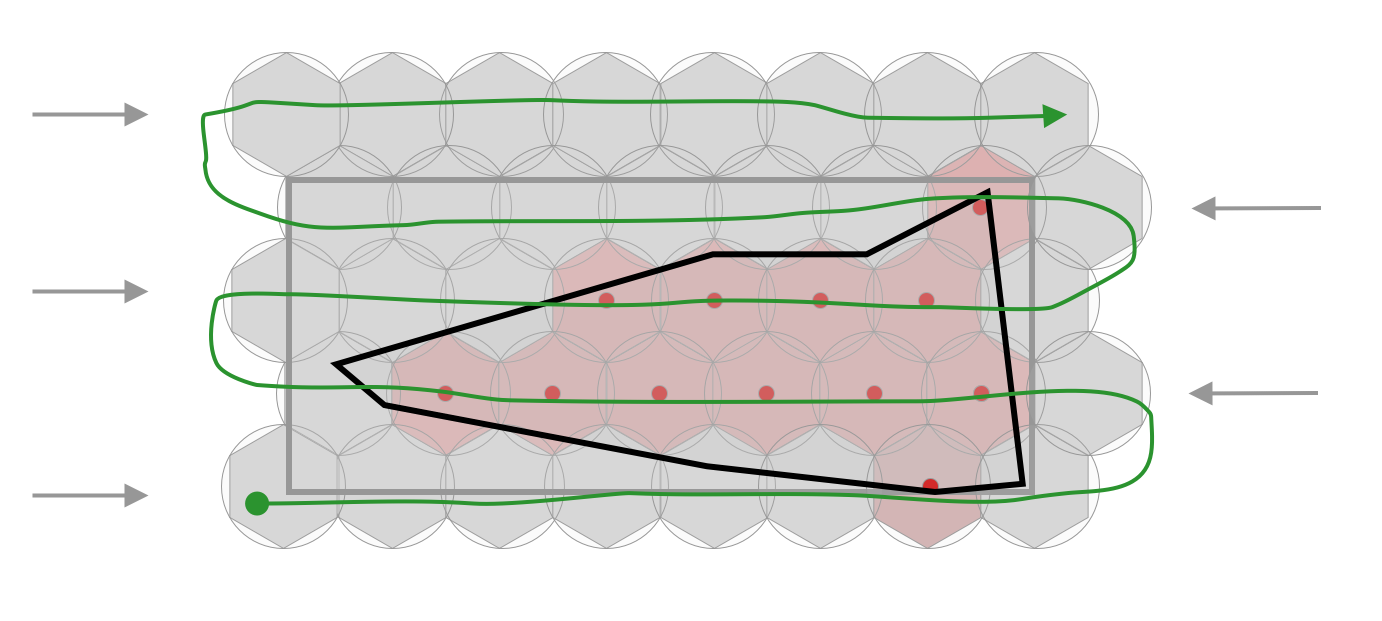
The Solution

Here began the most interesting part. As usual, the idea is the main thing, but the realization is the most interesting.

According to our idea, there is must be a few steps, that should be done before we actually can get the result.

Define the polygon area to be covered

At first look, this is a simple task - the user can just tap on the map and select the area, so we just create a polygon from the input points.

But, if user pick points not one-by-one, or pick some points inside already selected area… As result, the polygon can be a bit unexpected:

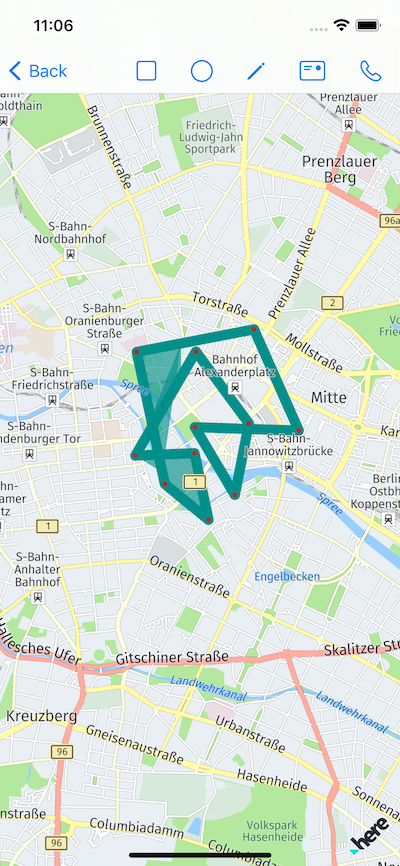
We can play a bit, and disable the points that are added by the user and already inside a polygon - the result will be a bit better, but, the order of newly added points can be still confusing, so additional kinds of sorting and arranging points may require.

There are a lot of algorithms that can help us to solve this problem. I decided to go with convex hull.

“The convex hull is a polygon with the shortest perimeter that encloses a set of points. As a visual analogy, consider a set of points as nails in aboard. The convex hull of the points would be like a rubber band stretched around the outermost nails.”

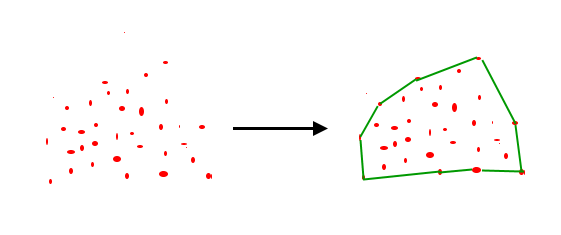
source of the image

My solution for this based on open-source solution from Rosseta:

protocol ConvexHullPoint: Equatable {
  var x: Double { get }
  var y: Double { get }
}

final class ConvexHull<T> where T: ConvexHullPoint {
  private enum Orientation {
    case straight
    case clockwise
    case counterClockwise
  }
  
  // MARK: - Public
  
  public func calculateConvexHull(fromPoints points: [T]) -> [T] {
    guard points.count >= 3 else {
      return points
    }
    
    var hull = [T]()
    let (leftPointIdx, _) = points.enumerated()
      .min(by: { $0.element.x < $1.element.x })!
    
    var p = leftPointIdx
    var q = 0
    
    repeat {
      hull.append(points[p])
      
      q = (p + 1) % points.count
      
      for i in 0..<points.count where
        calculateOrientation(points[p], points[i], points[q]) == .counterClockwise {
        q = i
      }
      
      p = q
    } while p != leftPointIdx
        
    return hull
  }
  
  // MARK: - Private
  
  private func calculateOrientation(_ p: T, _ q: T, _ r: T) -> Orientation {
    let val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y)
    
    if val == 0 {
      return .straight
    } else if val > 0 {
      return .clockwise
    } else {
      return .counterClockwise
    }
  }
}

and to transformed modification to use with location:

import CoreLocation

public enum CoordinatesConvexHull {
  static public func convexHull(_ input: [CLLocationCoordinate2D]) -> [CLLocationCoordinate2D] {
    let sorter = ConvexHull<CLLocationCoordinate2D>()
    return sorter.calculateConvexHull(fromPoints: input)
  }
}

extension CLLocationCoordinate2D: ConvexHullPoint {
  
  public static func == (lhs: CLLocationCoordinate2D, rhs: CLLocationCoordinate2D) -> Bool {
    lhs.latitude == rhs.latitude && lhs.longitude == rhs.longitude
  }

  var x: Double {
    latitude
  }
  
  var y: Double {
    longitude
  }
}

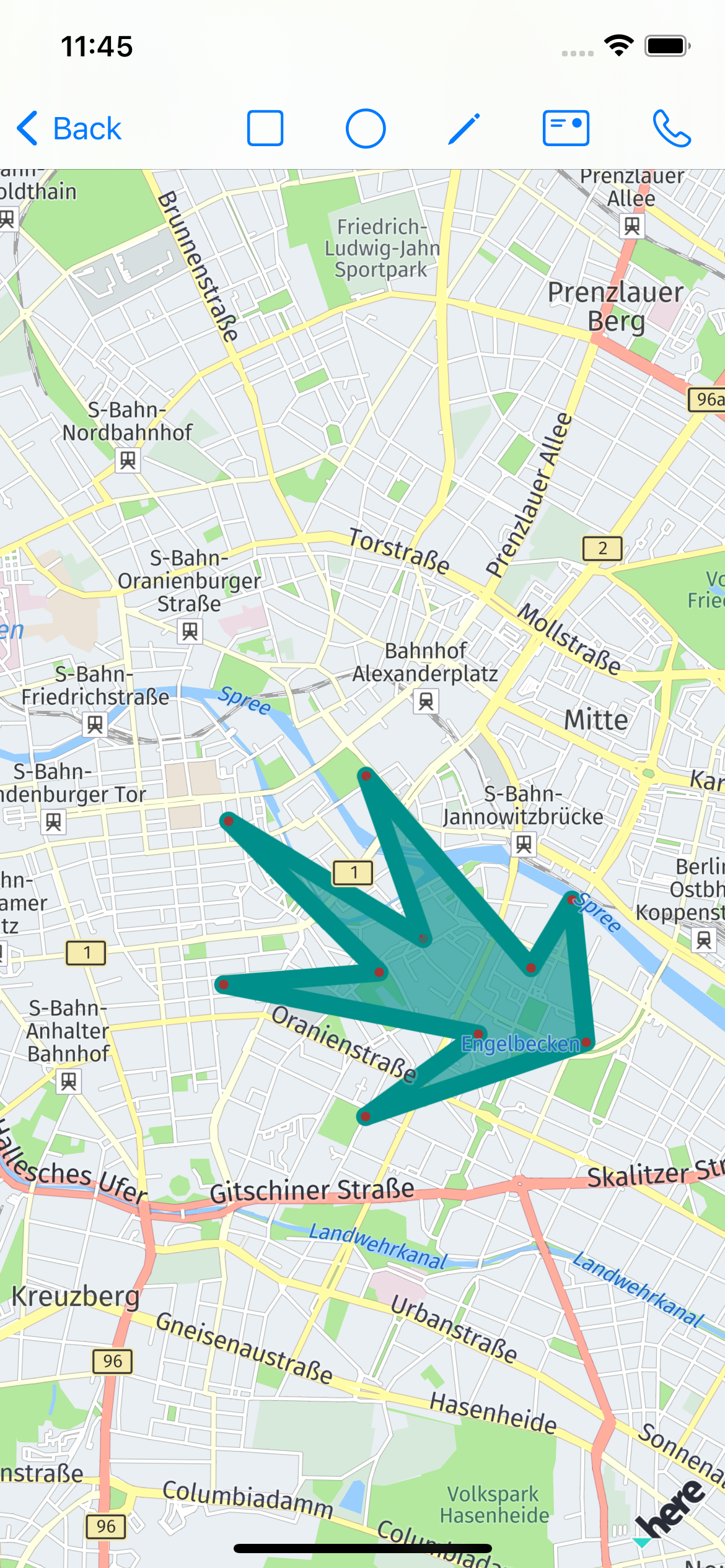
The result of this can be shown on map as:

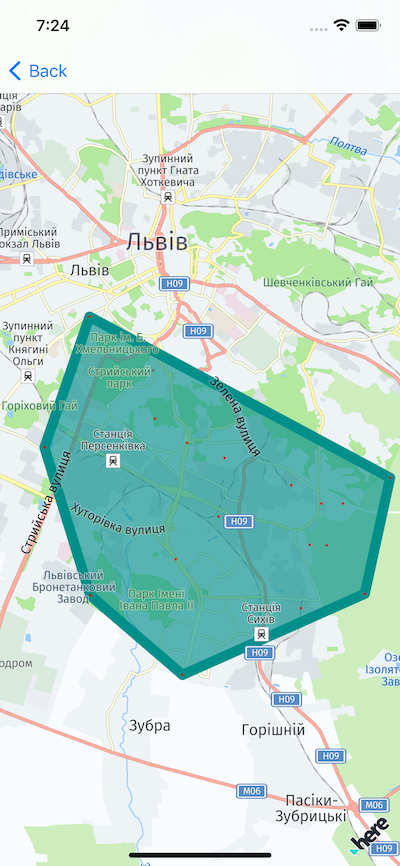
Various approaches have a different downside. For the selected algorithm this will be the limited possibilities of the selected zone. U actually can’t create a polygon with an acute angle. Selecting a new algorithm may be a good point for improvements.

Define the parameters of the shape to be used as covering shape

If we look back, we can see, that this step is already determined.

To summarize, here is the list of the required data for us:

1) A set of points to be processed for created proper polygon 2) Area definition and unit system definition for polygons that will be used for covering picked by user location

Cover the full area with hexagon

This is a very interesting step.

As u read earlier, to follow our idea, we should define a bounding box for picked polygon, and then, starting from one corner fill this bounding box with hexagons, saving the center of each hexagon as a possible center for our covering shapes.

Bounding box

To determine the bounding box, we should think about Earth, and how it is represented on a map. The cylindrical projection is used in most maps, another name for it - Mercator map.

source

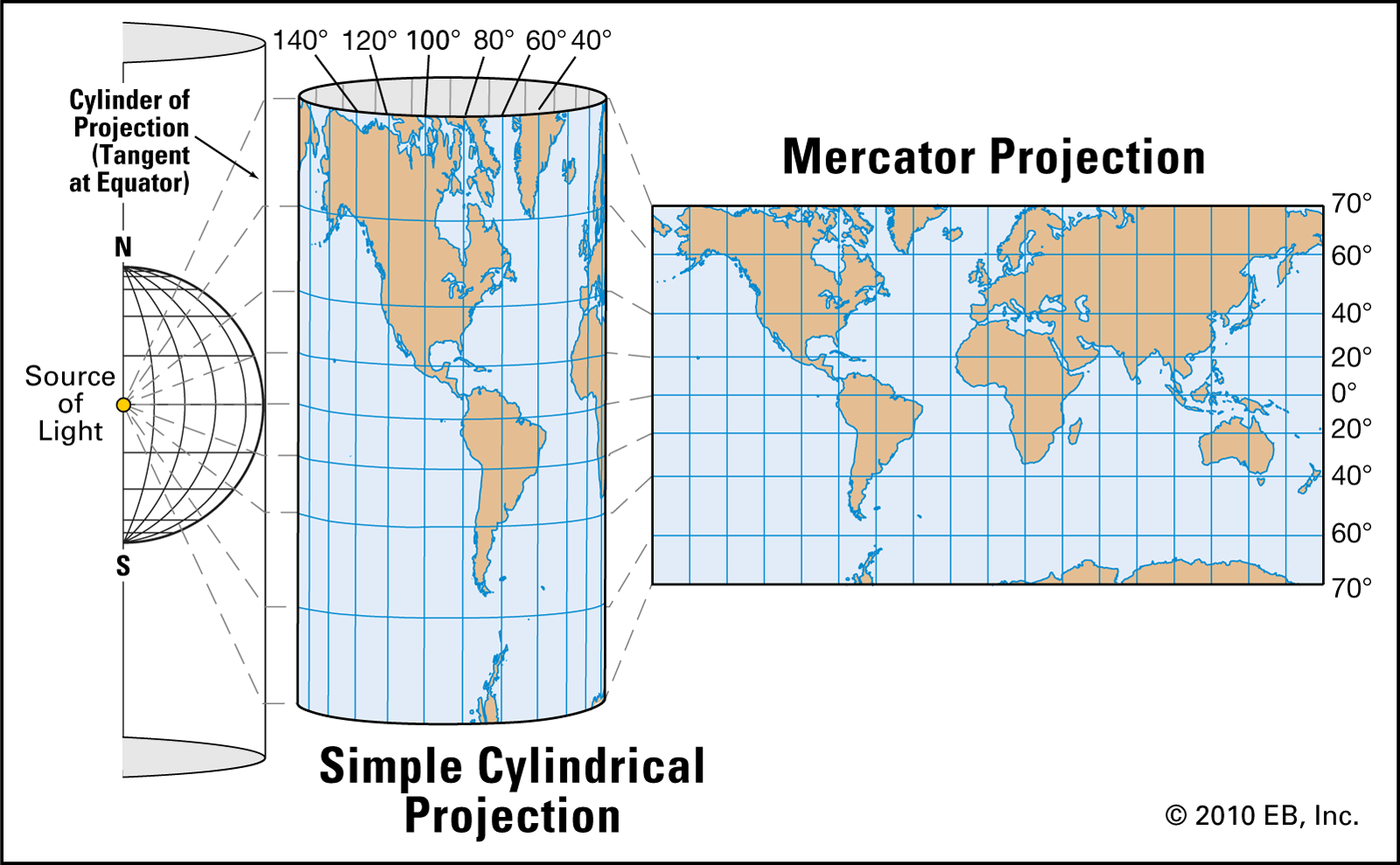
For us, this is good, because as u can see - it’s just a 2D coordinate system, so we should find only 2 points to make the job done.

We can use an existing API from MapKit and found MKCoordinateRegion, and then convert it to the bounding box, as it’s described here or here, but, I think, then pure solution a bit better - it can provide a clear vision of how it works for us, so understanding of the process will be much better.

I used GeoTools from wpearse as a base point, and have prepared a swift version of boundingBox.

Instead of naming like topLeft, bottomRight etc corners, for map better to use combination of East West South and North. To better understand this, here is the compas:

The code for finding bounding box should simply define min values for each corners and iterate througth all points by comparing lat/long to initial value. In case of difference store the new value if needed as minimum:

if coordinate.latitude > _northEastCorner.latitude {
  _northEastCorner.latitude = coordinate.latitude
}
if coordinate.longitude > _northEastCorner.longitude {
  _northEastCorner.longitude = coordinate.longitude
}
    
if coordinate.latitude < _southWestCorner.latitude {
  _southWestCorner.latitude = coordinate.latitude
}
if coordinate.longitude < _southWestCorner.longitude {
  _southWestCorner.longitude = coordinate.longitude
}

the full source code available in the download section at the end of the article

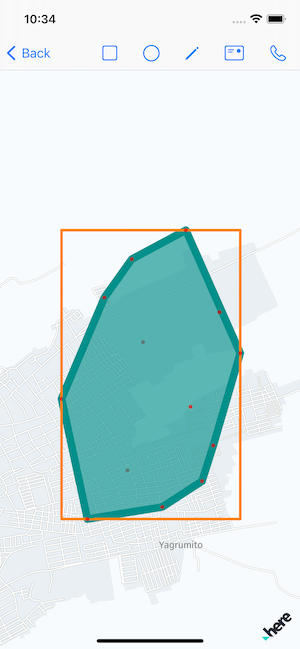
Always check different lat/long for any work related to the map.

Making hexagon mask for area

Now, when we have a bounding box, we should cover it with hexagons.

Everything u need to know about hexagon grids can be found at this ultimate guide.

The idea is to get the southWest corner, then move to the east and north.

The naive approach (my first attempt) can be next - we can think about bounding box as a regular rect (thus our map Mercator is 2D).

// get the bounding box
let bbox = GeoBoundingBox()
bbox.appendPoints(points)
    
let bottomLeft = bbox.southWestCorner
let topRight = bbox.northEastCorner
let bottomRight = bbox.southEastCorner

// get the size of polygon for covering    
let approxCirclePolygonRadius: CLLocationDegrees = (polygonSideSizeInMeters / 2).toDegree // <- the problem part 1

// found the bounds of covering area (a bit biggger then bounding box)    
let latLimit = topRight.latitude + 2 * approxCirclePolygonRadius //vertical
let longLimit = bottomRight.longitude + 2 * approxCirclePolygonRadius // horizontal

// grid height = 0.75 * height of hexagon    
let gridHeight = 2 * approxCirclePolygonRadius * 0.75

// store poposed centers    
var proposedCenters: [CLLocationCoordinate2D] = []

// initial coordinates    
var currentLong = bottomLeft.longitude
var currentLat = bottomLeft.latitude
    
// thus this is hexagon grid, one line will be shifter to the right
// so, first, determine all lines without shift
// in next iteration all hexagon lines, that are shifted    
while currentLat < latLimit {
  currentLong = bottomLeft.longitude
  
  while currentLong < longLimit {
    let centerPoint = CLLocationCoordinate2D(latitude: currentLat, longitude: currentLong)
    proposedCenters.append(centerPoint)
    currentLong += 2 * gridHeight
  }

  // append latitude to move aka horizontally in bounding box
  currentLat += 2 * approxCirclePolygonRadius // <- the problem part 2
}
    
currentLong = bottomLeft.longitude - gridHeight / 2.0
currentLat = bottomLeft.latitude + approxCirclePolygonRadius * 2
    
while currentLat < latLimit {
  currentLong = bottomLeft.longitude - gridHeight / 2.0
  
  while currentLong < longLimit {
    let centerPoint = CLLocationCoordinate2D(latitude: currentLat, longitude: currentLong)
    proposedCenters.append(centerPoint)
    currentLong += 2 * gridHeight
  }

  currentLat += 2 * approxCirclePolygonRadius
}

Other approaches of how to calculate grid can be found here

As u can see, we should somehow convert meters into degrees (toDegree computed prop.) and add diff in latitude to the coordinate, to find the next center of the hexagon.

To better understand how latitude and logitude works, here is the small reference:

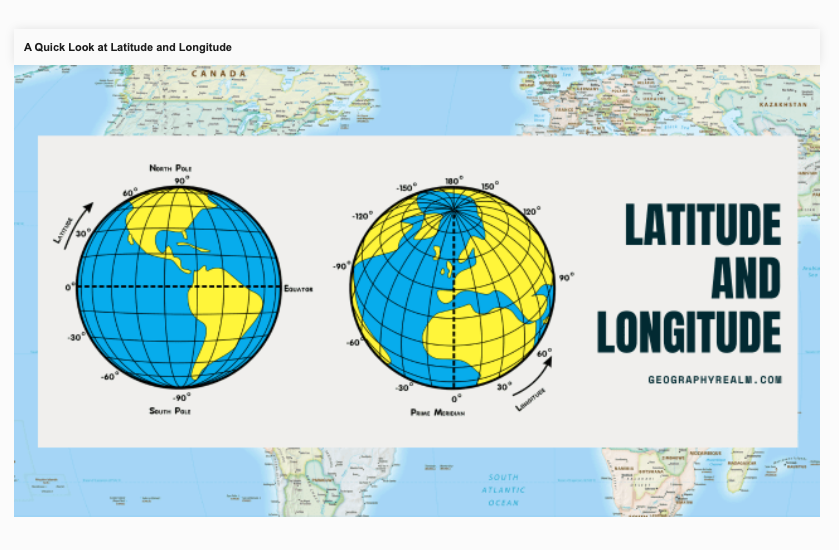
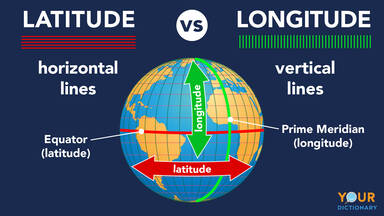
My first thing was - “I can use average value”, so, I decided to use average Earth radius for all latitudes

var toDegree: CLLocationDegrees {
    let earthRadiusInMeters = 6378137.0
    let oneDegreeToMeter = (2 * Double.pi * earthRadiusInMeters * 1) / 360.0
    let value: CLLocationDegrees = self / oneDegreeToMeter
    return value
}

The result was, that on different locations (depends from latitude) the offset between hexagons are different. If I would like to have 50m between centers, I can get from 32m to 121m:

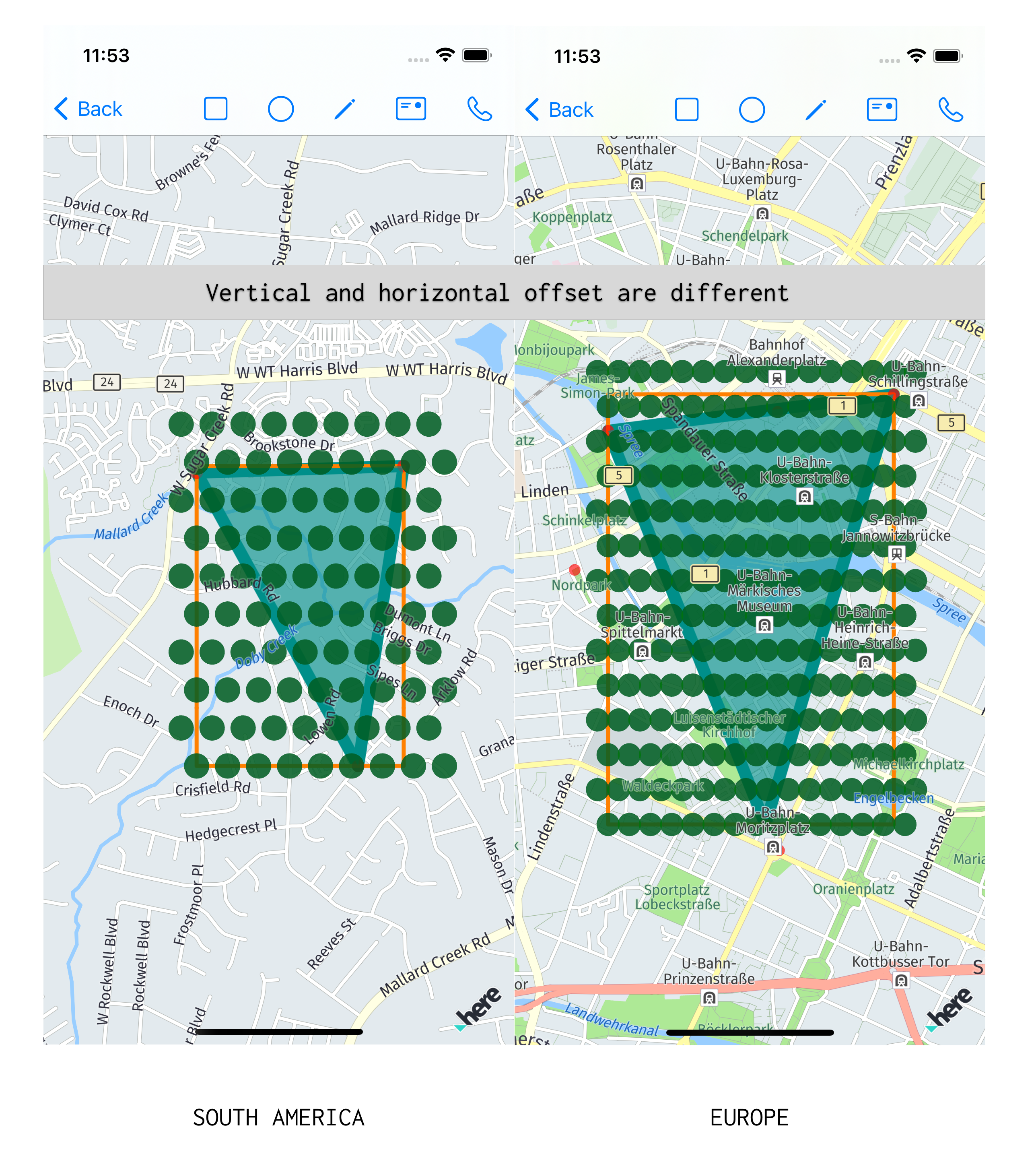
Thus I used the average radius of the Earth, I tried to remove this inconsistency. To do so, I read about ways how to calculate Earth’s radius.

The first try was to use some koef for different latitude:

func toDegreeAt(latitude: CLLocationDegrees) -> CLLocationDegrees {
	// koef for diff values of the latitude
	// describe the radius of Earth on selected lat
	  
	let quotient: Double
	let latitudeDegreeMod = abs(floor(latitude))
	    
	if latitudeDegreeMod == 0 {
	  quotient = 1.1132
	} else if latitudeDegreeMod <= 23 {
	  quotient = 1.0247
	} else if latitudeDegreeMod <= 45 {
	  quotient = 0.7871
	} else {
	  quotient = 0.43496
	}
	    
	return (self * 0.00001) / quotient
}

This gave a bit better result, so I decided to use a more precise method.

The formula for Earth radius calculation:

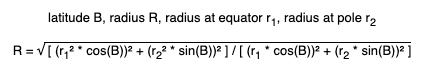
I translated it into the code:

let earthRadiusInMetersAtSeaLevel = 6378137.0
let earthRadiusInMetersAtPole = 6356752.314
    
let r1 = earthRadiusInMetersAtSeaLevel
let r2 = earthRadiusInMetersAtPole
let beta = latitude

let earthRadiuseAtGivenLatitude = (
  ( pow(pow(r1, 2) * cos(beta), 2) + pow(pow(r2, 2) * sin(beta), 2) ) /
  ( pow(r1 * cos(beta), 2) + pow(r2 * sin(beta), 2) )
)
.squareRoot()

But, the result was still not good - deviation was still present.

I read, that normally during navigatio a bearing is used - the horizontal angle between the direction of an object and another object source.

Reading this, I realize, that problem was a bit more complex - I should not just correct the distance by using a more precise calculation of Earth radius, but also use bearing during the next point calculation.

Here is a bearing reference:

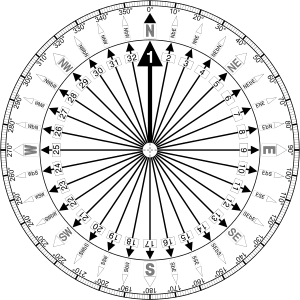
To represent bearing, I added simple struct:

extension CLLocationDegrees {
  enum Bearing {
    case up
    case right
    case down
    case left
    case any(CLLocationDegrees)
    
    var value: CLLocationDegrees {
      switch self {
        case .any(let bearingValue):
          return bearingValue
        case .down:
          return 180
        case .right:
          return 90
        case .left:
          return 270
        case .up:
          return 0
      }
    }
  }
}

Now, we can use current point and bearing to properly calculate the next point:

extension CLLocationCoordinate {
  func locationByAdding(
    distance: CLLocationDistance,
    bearing: CLLocationDegrees
  ) -> CLLocationCoordinate2D {
    let latitude = self.latitude
    let longitude = self.longitude
    
    let earthRadiusInMeters = self.earthRadius()
    let brng = bearing.degreesToRadians
    var lat = latitude.degreesToRadians
    var lon = longitude.degreesToRadians
    
    lat = asin(
      sin(lat) * cos(distance / earthRadiusInMeters) +
        cos(lat) * sin(distance / earthRadiusInMeters) * cos(brng)
    )
    lon += atan2(
      sin(brng) * sin(distance / earthRadiusInMeters) * cos(lat),
      cos(distance / earthRadiusInMeters) - sin(lat) * sin(lat)
    )
    
    let newCoordinate = CLLocationCoordinate2D(
      latitude: lat.radiansToDegrees,
      longitude: lon.radiansToDegrees
    )
    
    return newCoordinate
  }
}

The result was amazing:

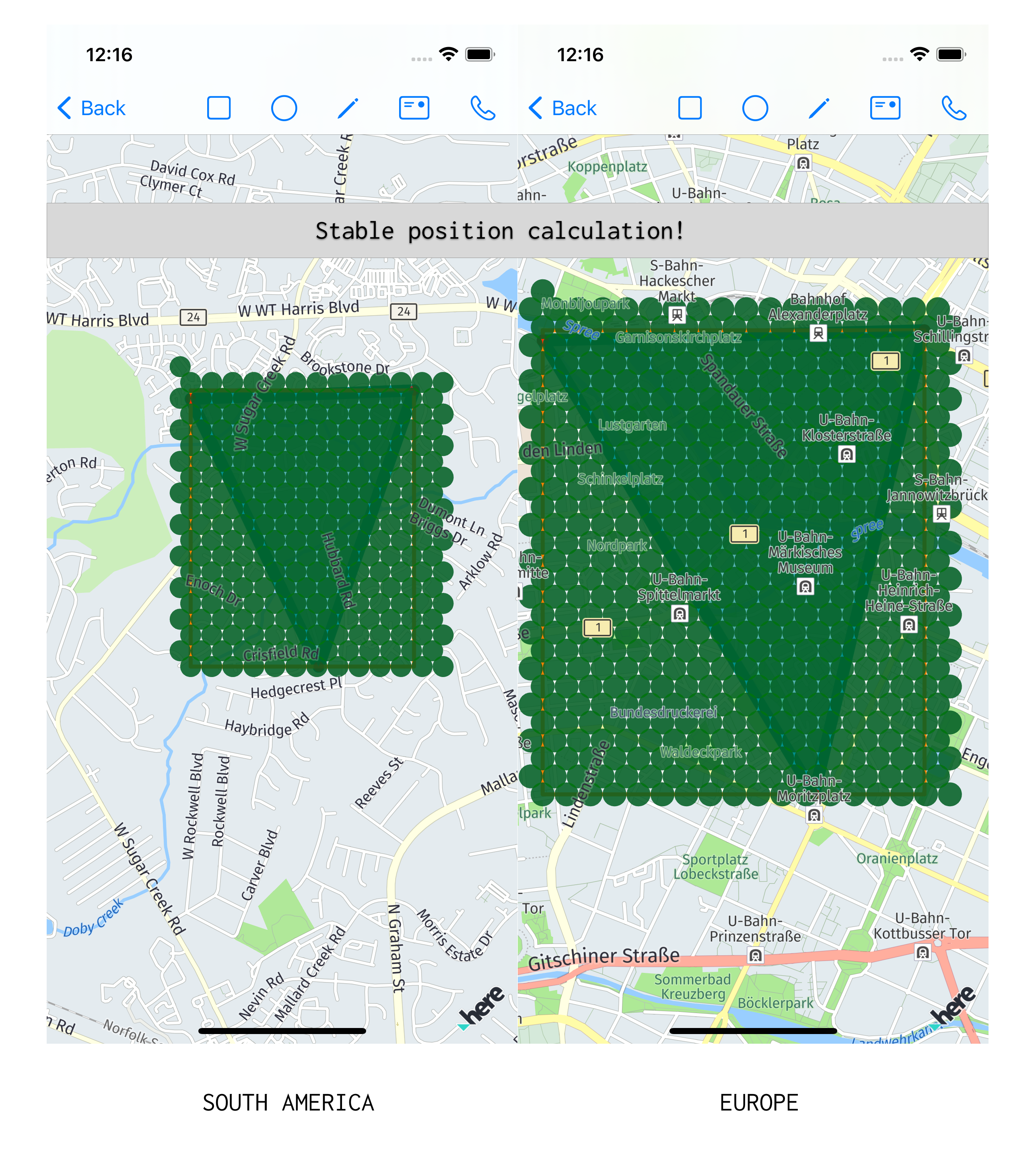
The final code:

let bbox = GeoBoundingBox()
bbox.appendPoints(points)
    
let bottomLeft = bbox.southWestCorner
let topRight = bbox.northEastCorner
let bottomRight = bbox.southEastCorner
    
var proposedCenters: [CLLocationCoordinate2D] = []
    
var currentLong = bottomLeft.longitude
let currentLat = bottomLeft.latitude
    
var centerPoint = CLLocationCoordinate2D(latitude: currentLat, longitude: currentLong)
proposedCenters.append(centerPoint)
    
let offsetPoint = centerPoint.locationByAdding(
  distance: 1,
  bearing: CLLocationDegrees.Bearing.right.value
)
let deegreePerMeter = abs(offsetPoint.longitude - centerPoint.longitude)
let degreeOffsetForCurrentArea = polygonSideSizeInMeters * deegreePerMeter
let gridHeight = degreeOffsetForCurrentArea * 0.75
    
let latLimit = topRight.latitude + gridHeight //vertical
let longLimit = bottomRight.longitude + degreeOffsetForCurrentArea / 2 // horizontal

var isEven = true
while centerPoint.latitude < latLimit {
  while centerPoint.longitude < longLimit {
    centerPoint = centerPoint.locationByAdding(
      distance: polygonSideSizeInMeters,
      bearing: CLLocationDegrees.Bearing.right.value
    )
    proposedCenters.append(centerPoint)
  }
  
  centerPoint = centerPoint.locationByAdding(
    distance: polygonSideSizeInMeters * 0.75,
    bearing: CLLocationDegrees.Bearing.up.value
  )
  centerPoint.longitude = bottomLeft.longitude +
                          (isEven ? -degreeOffsetForCurrentArea / 2 : 0)
  proposedCenters.append(centerPoint)
  currentLong = centerPoint.longitude
  
  isEven.toggle()
}

Determine what centers of shapes are inside of your initial polygon and select them

Now, the last part - is to determine what exactly hexagons are needed.

To do so, I created a simple protocol, that may represent the required logic:

public protocol PolygonFilter {
  init(polygonCoordinates: [CLLocationCoordinate2D])
  func filter(_ coordinate: CLLocationCoordinate2D) -> Bool
}

Thus, I used polygons and Maps, I know, that MapKit polygon can provide such functionality, so one of the filters may be based on MKPolygon logic.

This is not ideal, I’m planning to replace convex hull algorithm to more precise and, based on new algorithm use new PolygonFilter

The code for MKPolygonFilter:

extension MKPolygon {
  func contain(coordinate: CLLocationCoordinate2D) -> Bool {
    let polygonRenderer = MKPolygonRenderer(polygon: self)
    let currentMapPoint: MKMapPoint = MKMapPoint(coordinate)
    let polygonViewPoint: CGPoint = polygonRenderer.point(for: currentMapPoint)
    return polygonRenderer.path?.contains(polygonViewPoint) == true
  }
}

struct MKPolygonFilter: PolygonFilter {
  let polygonCoordinates: [CLLocationCoordinate2D]
  let polygon: MKPolygon
  
  init(
    polygonCoordinates: [CLLocationCoordinate2D]
  ) {
    self.polygonCoordinates = polygonCoordinates
    self.polygon = MKPolygon(coordinates: polygonCoordinates, count: polygonCoordinates.count)
  }

  func filter(_ coordinate: CLLocationCoordinate2D) -> Bool {
    polygon.contain(coordinate: coordinate)
  }
}

And the usage:

// introduce new enum type and pass as a param

public enum Filter {
	case mkPolygon
	case any(PolygonFilter.Type)
	    
	var instanceType: PolygonFilter.Type {
	  switch self {
	    case .mkPolygon:
	      return MKPolygonFilter.self
	    case .any(let returnType):
	      return returnType
	  }
	}
}

// after all hexagon centers calculation
let filtrator = filter.instanceType.init(polygonCoordinates: points)
let filtered = proposedCenters.filter(filtrator.filter) // <- needed hexagons

The result:

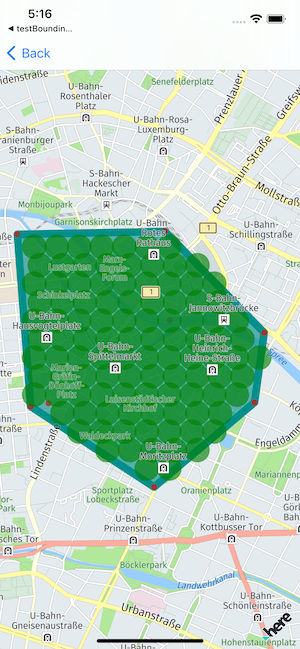
Demo

The full demo:

Covering an arbitary area with Circles of equal radius

The problem

The Idea

The Solution

Define the polygon area to be covered

Define the parameters of the shape to be used as covering shape

Cover the full area with hexagon

Bounding box

Making hexagon mask for area

Determine what centers of shapes are inside of your initial polygon and select them

Demo

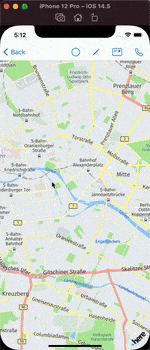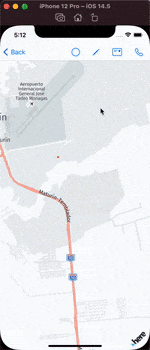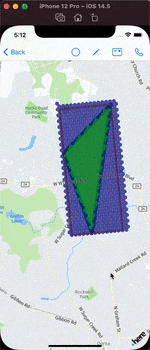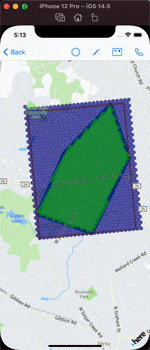
Resource

Convex hull

Bounding box

Hexagon grid

Map tools online