Polygon Area calculation

The code
Resources:

On my current project, I have a few tasks related to maps. It’s all very interesting - mercator, global positioning, area calculation, bearing, and other stuff.

In this post, I would like to share an approach how to calculate the area for the selected polygon.

There are a lot of algorithms, that can be used to determine the correct value for the area.

I read a bit and found a good paper about it, so the algorithm is based on “Some Algorithms for Polygons on a Sphere” by Chamberlain & Duquette (JPL Publication 07-3, California Institute of Technology, 2007).

The code

As input, we should accept points for polygon - any area that the user can select. It’s good to mention, that all calculations are done in a metric system, using “meter” as a base value.

Steps:

1) Check the number of points - if <2 - nothing to do, return 0 2) calculate the area of each sector and sum them 3) convert square Meters to required units

The solution can be next:

  public static func area(
    for coordinates: [CLLocationCoordinate2D],
    formattedTo outputUnit: UnitArea = .squareMeters
  ) -> Double {
// step 1
    guard coordinates.count > 2 else {
      return 0
    }
    
// step 2
    let earthRadiusInMeters = 6378137.0
    var totalArea = 0.0
    
    for i in 0..<coordinates.count {
      let p1 = coordinates[i > 0 ? i - 1 : coordinates.count - 1]
      let p2 = coordinates[i]
      
      totalArea += (p2.longitude.degreesToRadians - p1.longitude.degreesToRadians) *
        (2 + sin(p1.latitude.degreesToRadians) + sin(p2.latitude.degreesToRadians))
    }
    totalArea = -(totalArea * earthRadiusInMeters * earthRadiusInMeters / 2)
    
    // to skip polygon definition - clockwise or counter-clockwise
    let squareMetersAreaValue = max(totalArea, -totalArea)

// step 3
    let squareMetersValueUnit = Measurement(
      value: squareMetersAreaValue,
      unit: UnitArea.squareMeters
    )
    
    let returnValue = squareMetersValueUnit.converted(to: outputUnit)
    return returnValue.value
  }

For validation we can use one of the online tools, like this

We also can improve a bit this calculation by adding a more precise calculation for Earth radius:

extension CLLocationCoordinate2D {
  
  func earthRadius() -> CLLocationDistance {
    let earthRadiusInMetersAtSeaLevel = 6378137.0
    let earthRadiusInMetersAtPole = 6356752.314
    
    let r1 = earthRadiusInMetersAtSeaLevel
    let r2 = earthRadiusInMetersAtPole
    let beta = latitude.degreesToRadians
    
    let earthRadiuseAtGivenLatitude = (
      ( pow(pow(r1, 2) * cos(beta), 2) + pow(pow(r2, 2) * sin(beta), 2) ) /
        ( pow(r1 * cos(beta), 2) + pow(r2 * sin(beta), 2) )
    )
    .squareRoot()
    
    return earthRadiuseAtGivenLatitude
  }
}

This calculation used in my prev post

The result:

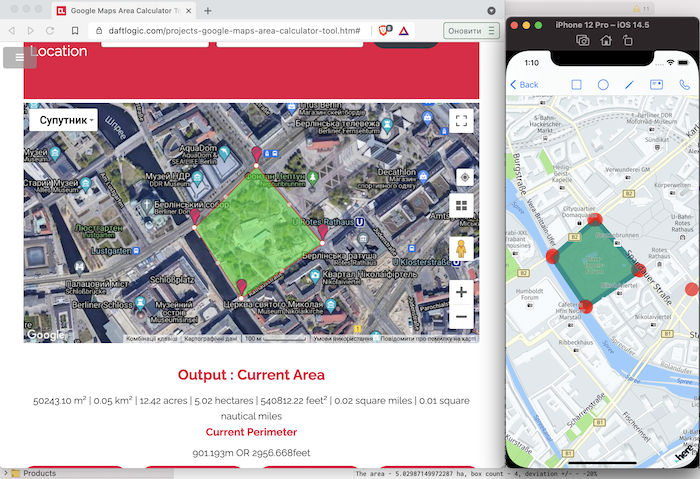
Another point for improving - may be additional usage of latitude for the selected region. I didn’t include this into the calculation (yet?)

The code

Resources: