As mobile developers, we should always think not only about the correctness of the logic but also about usability (UX) and about different ways, that can reduce the number of errors when we receive user input (kind of Poka-yoke ポカヨケ).

In this post, I would like to describe the process of how we can improve the polygon selection for the area on the map (by removing polygon side interactions).

I already wrote about some techniques related to the map that was used on my current project (like this post about area coverage or this one about area calculation).

Current post can be used as an improvement for area coverage - the first step of the process described there.

The Problem

If the user defines the polygon on the map, then, it’s the user’s responsibility to correctly determine the polygon and every point of it. But, the standard way of creating a polygon - is just to combine all points one-by-one into some structure, without checking if the new point intersects the already created side of the polygon or no.

Such behavior works fine, if the user precise enough, but, in some cases, this can cause a problem - the polygon gets an unexpected shape.

As always - one image much better than thousend word:

idea



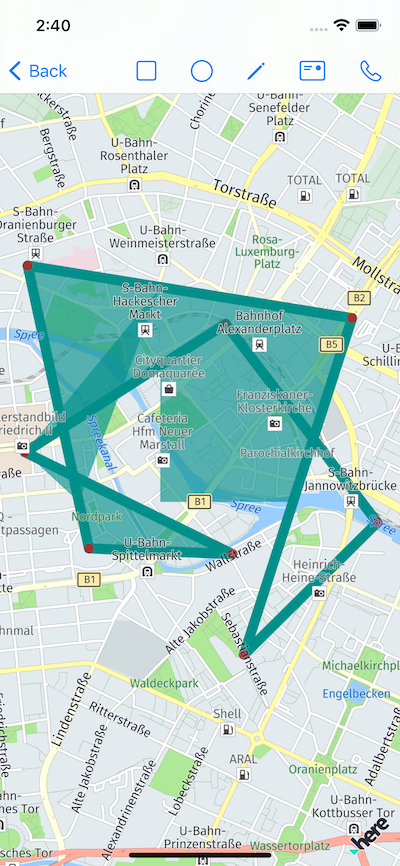
The Solution

Note - nothing new in this article is discovered - I just want to summarise my experience in solving this problem.

As a solution we can restrict the selection of points for polygon, that, in combination with any of the existing points in the polygon, can create a line (polyline) intersection with our polygon. In other words - we should check all possible lines (combination of any 2 points) in polygon for a possible intersection.

This means, that we should:

  • Determine all possible lines combination from polygon
  • Check whenever any combination of 2 lines segments (from step1) can intersect

Obviously - not the most efficient method - complexity of this is about O(nˆ2). While our polygon not very big and complex, we can use it. In another case, we may want to improve the process.

Determine all possible lines combination from polygon

At the first look, this part is not very complicated - all that needs to be done is to iterate through all points and create all combinations of them (all possible segments). Thus for a line, we need 2 points, we should create 2 iterations.

This naive approach can look like a simple for-each loop where input is a points: [CLLocationCoordinate2D]

(1..<points.count - 1).forEach { i in
 (0 ..< i-1).forEach { j in
    // points for 2 lines
   let p0 = points[i]
   let p1 = points[i+1]
   let p2 = points[j]
   let p3 = points[j+1]
   // check intersection
 }
}

Then - just to check whenever 2 segments are intersected.

The result at first looks fine:

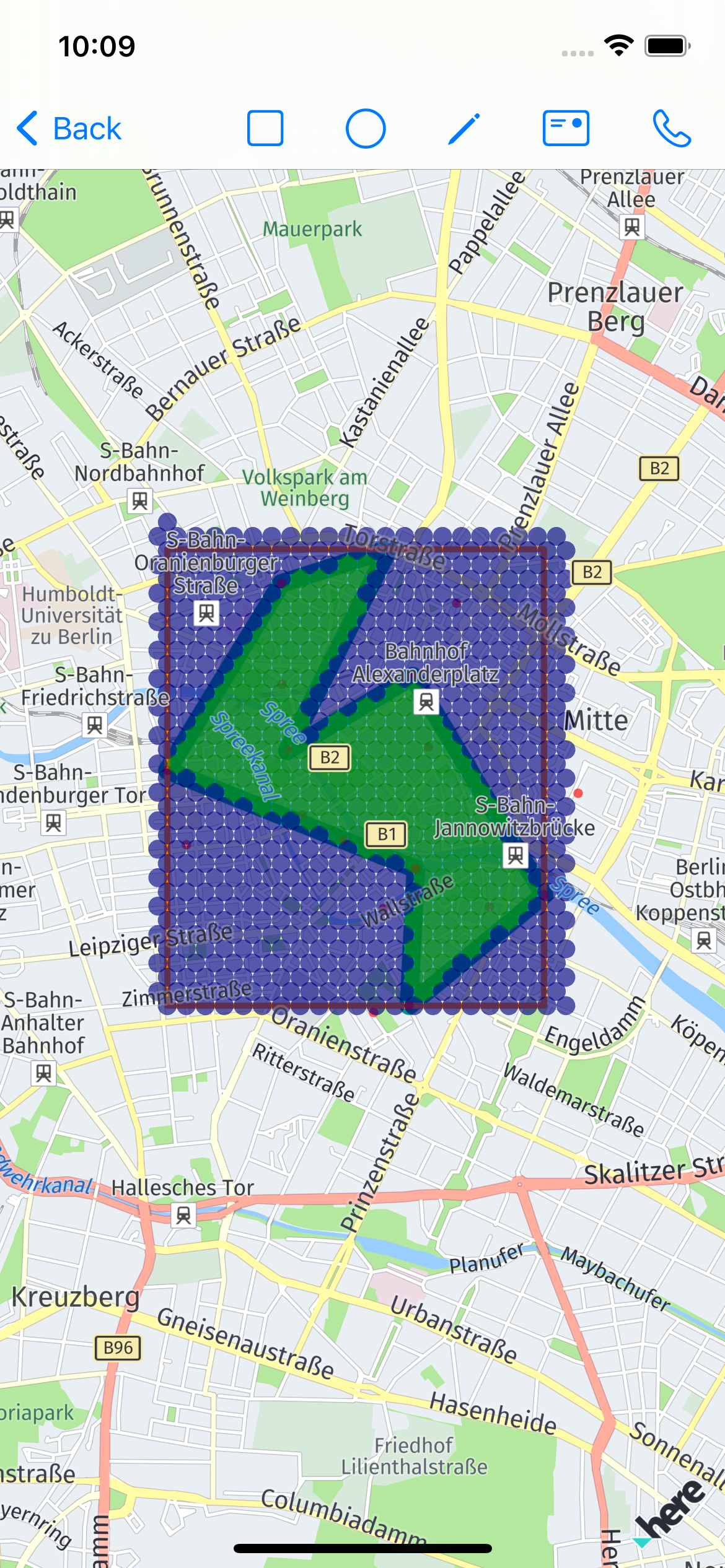
linesegments



But, as soon, as user pick a bit tricky polygon, we can get this:

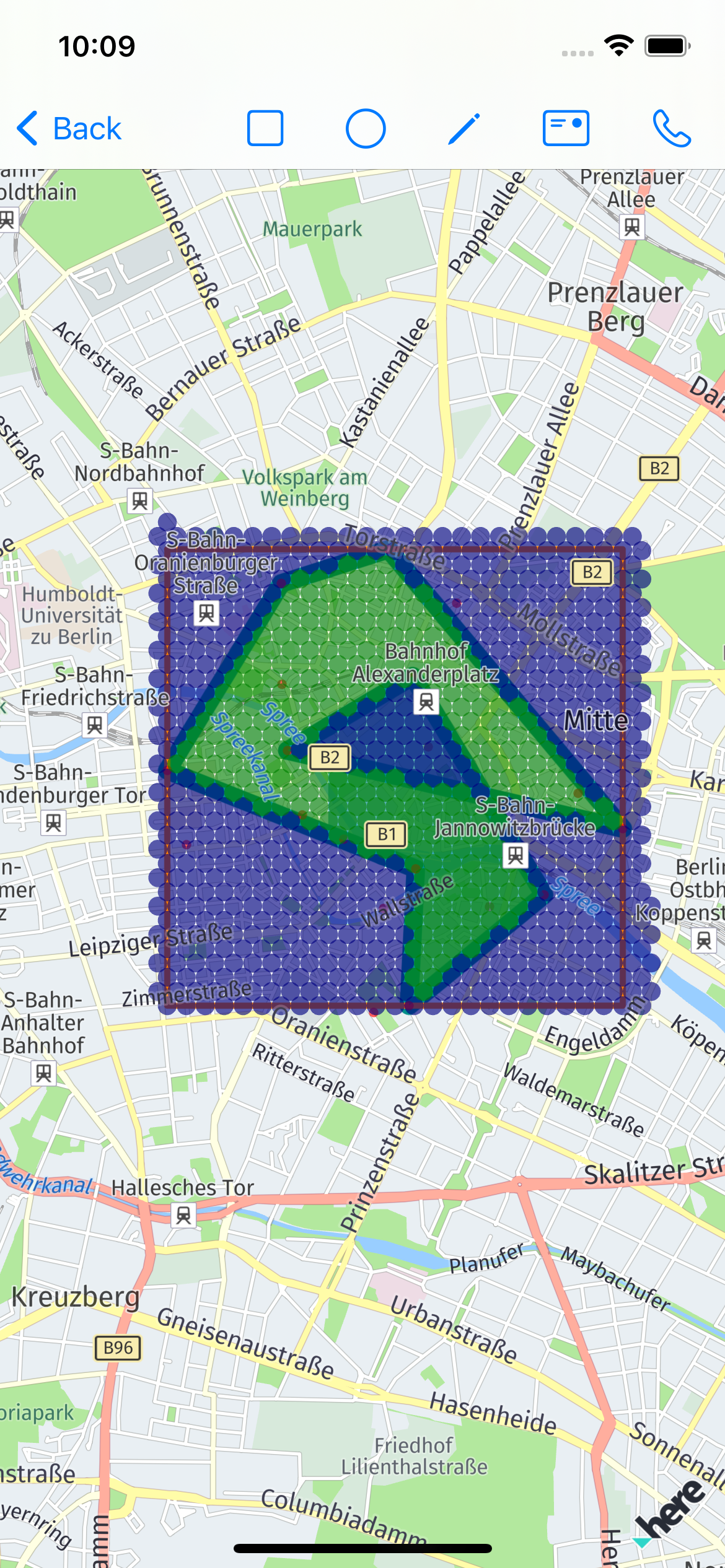
linesegments



The problem here - is because we check all segments for the existing polygon within the new segment, except the last segment - between the new point and first point.

This means, that we should modify the loop, we should create 2 segments using a new point - for last and for the first point in the polygon point’s list and then check intersection with all segments present in the polygon.

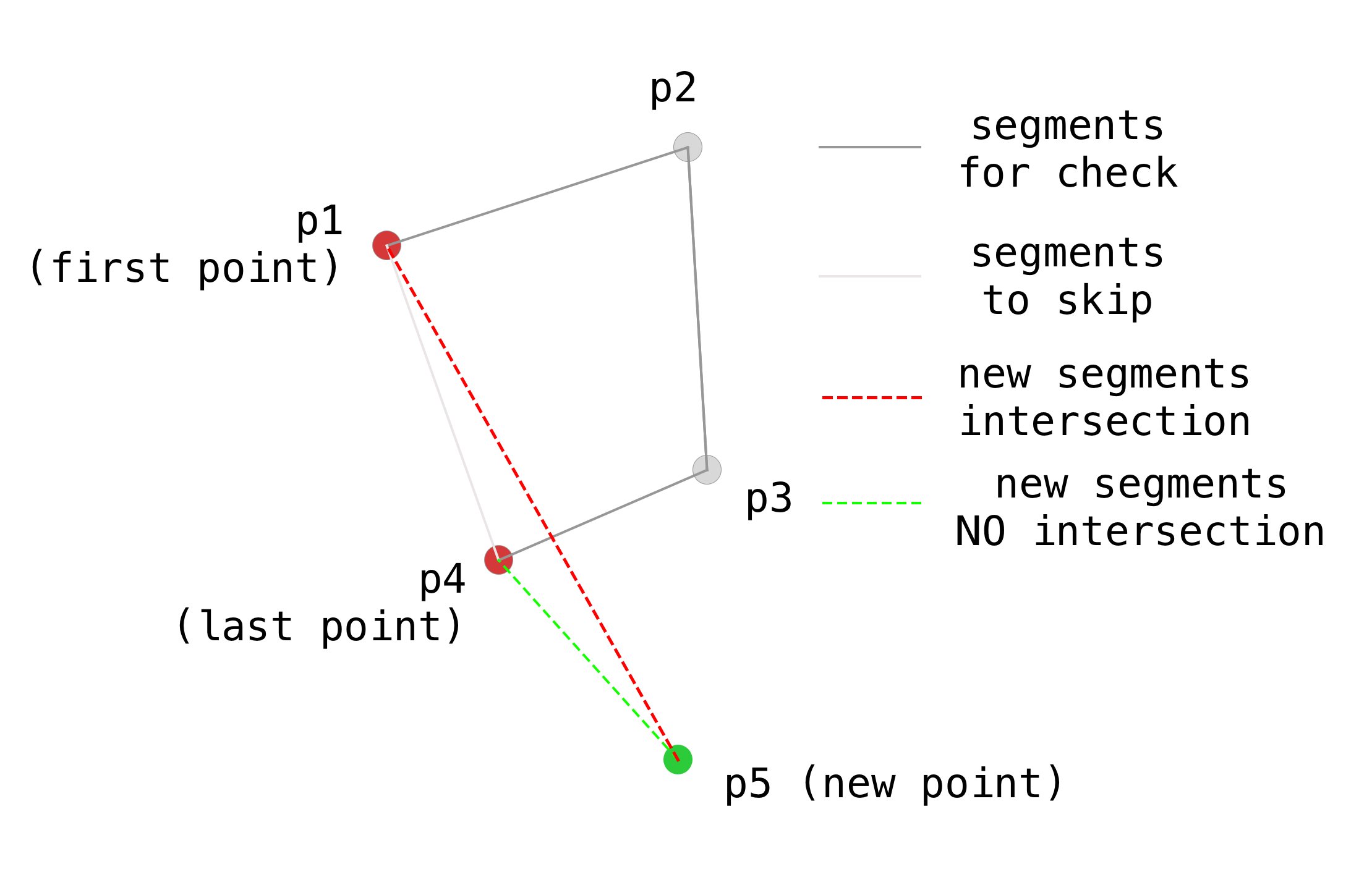
intersection_tests



Within the previous approach segment p1-p5 was not included in the check

The code could looks like this:

    var intersections: [CLLocationCoordinate2D] = []
    if polygonPoints.count < 3 {
      return intersections
    }

    var segments: [(CLLocationCoordinate2D, CLLocationCoordinate2D)] = []
    for i in 0..<polygonPoints.count-1 {
      let segmentPoint1 = polygonPoints[i]
      let segmentPoint2 = polygonPoints[i+1]
      segments.append((segmentPoint1, segmentPoint2))
    }

    let newSegmentToLastPoint = (polygonPoints[polygonPoints.count-1], aPoint)
    let newSegmentToFirstPoint = (polygonPoints[0], aPoint)

    [
      newSegmentToLastPoint,
      newSegmentToFirstPoint
    ]
    .forEach { newSegment in
      segments.forEach { existingSegments in
        if let intersection = // somehow {
          if !polygonPoints.contains(intersection) {
            intersections.append(intersection)
          }
        }
      }
    }
    
    return intersections

We check all segments for intersection and exclude points, that already a corners for polygon

Check if 2 lines segments intersect

Looking for a solution, I found a very interesting comment from Gavin. He mentions, that there is a book by Andre LeMothe’s “Tricks of the Windows Game Programming Gurus” with an algorithm, that solve this problem. The code that he puts there works fine, but I would like to know how it works before actually use.

Here is the code:

func lineIntersection(
  p0_x: Double, p0_y: Double,
  p1_x: Double, p1_y: Double,
  p2_x: Double, p2_y: Double,
  p3_x: Double, p3_y: Double
) -> (x: Double, y: Double)? {
  let s1_x: Double
  let s1_y: Double
  let s2_x: Double
  let s2_y: Double
  
  s1_x = p1_x - p0_x
  s1_y = p1_y - p0_y
  
  s2_x = p3_x - p2_x
  s2_y = p3_y - p2_y
  
  let s: Double
  let t: Double
  s = (-s1_y * (p0_x - p2_x) + s1_x * (p0_y - p2_y)) / (-s2_x * s1_y + s1_x * s2_y);
  t = ( s2_x * (p0_y - p2_y) - s2_y * (p0_x - p2_x)) / (-s2_x * s1_y + s1_x * s2_y);
  
  if (s >= 0 && s <= 1 && t >= 0 && t <= 1) {
    let i_x = p0_x + (t * s1_x);
    let i_y = p0_y + (t * s1_y);
    return (i_x, i_y)
  }
  
  return nil
}

To simplify usage with map

func lineIntersectionOnMap(
  p0: CLLocationCoordinate2D,
  p1: CLLocationCoordinate2D,
  p2: CLLocationCoordinate2D,
  p3: CLLocationCoordinate2D
) -> Bool {
  lineIntersection(
    p0_x: p0.latitude, p0_y: p0.longitude,
    p1_x: p1.latitude, p1_y: p1.longitude,
    p2_x: p2.latitude, p2_y: p2.longitude,
    p3_x: p3.latitude, p3_y: p3.longitude
  ) != nil
}

How it works. In the mentioned above book, there is a very good explanation in chapter 13 “Intersection the Line segments”.

Here are a few images, that explain everything better than any words:

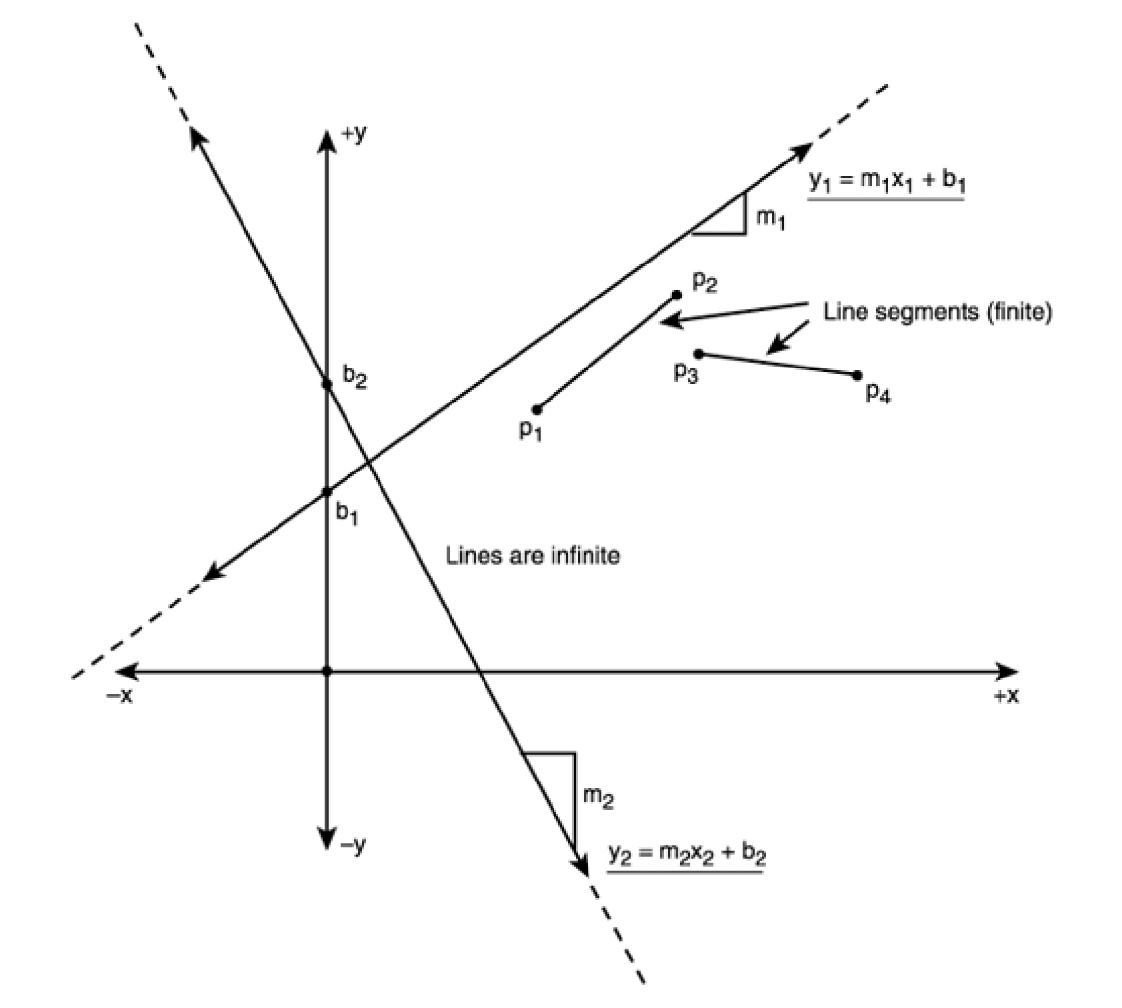
The difference between lines (infinite) and line segments (finite)

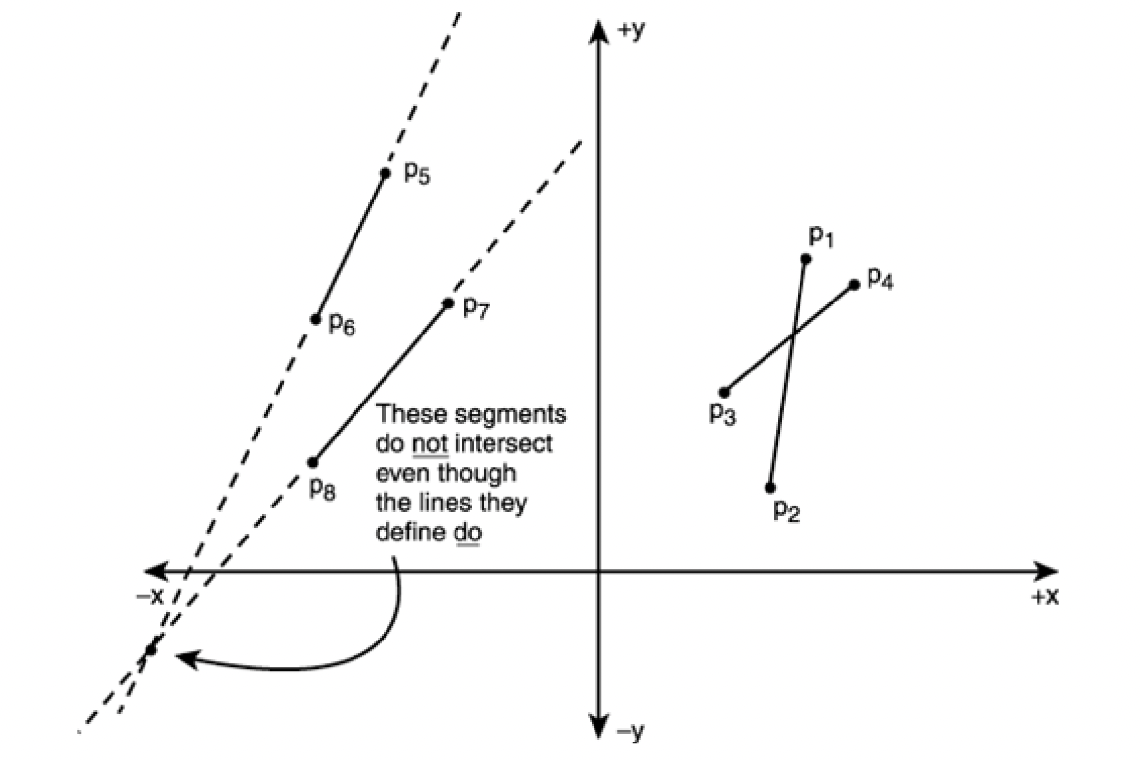
linesegments



Intersecting and non-intersection segments

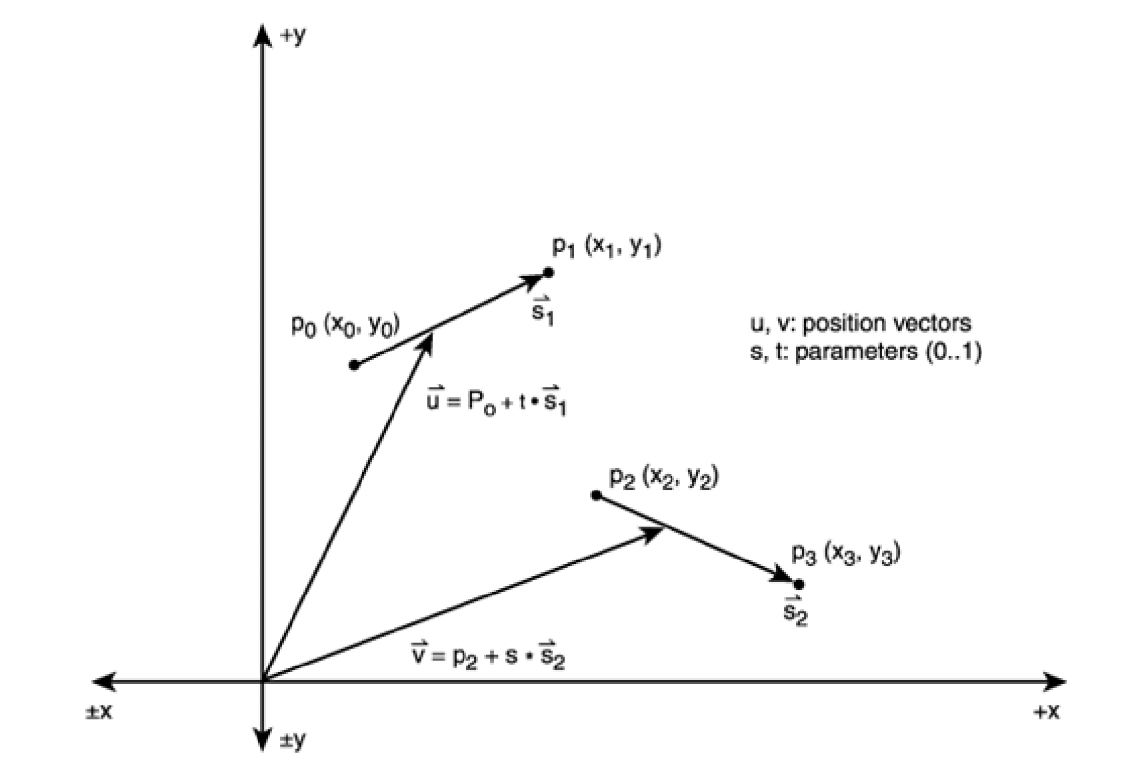
linesegments



To solve the problem used parametric representation of each line segment: U - the position vector of any point on line segment S1 and V same on segment S2:

linesegments



By using Cramer’s rule the author solved this task. I won’t copy the whole steps, just the final result (used in a code sample above):

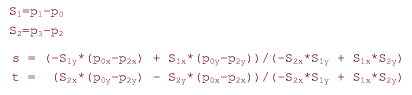
linesegments



Exactly these formulas used in the code above.

Slightly improved code, adjusted for use with coordinates:

  static func intersectPointForSegmentsWith(
    p0: CLLocationCoordinate2D,
    p1: CLLocationCoordinate2D,
    p2: CLLocationCoordinate2D,
    p3: CLLocationCoordinate2D
  ) -> CLLocationCoordinate2D? {
    
    var denominator = (p3.longitude - p2.longitude) * (p1.latitude - p0.latitude) -
      (p3.latitude - p2.latitude) * (p1.longitude - p0.longitude)
    
    let isCollinear = denominator == 0
    if isCollinear {
      return nil
    }
    
    var ua = (p3.latitude - p2.latitude) * (p0.longitude - p2.longitude) -
      (p3.longitude - p2.longitude) * (p0.latitude - p2.latitude)
    var ub = (p1.latitude - p0.latitude) * (p0.longitude - p2.longitude) -
      (p1.longitude - p0.longitude) * (p0.latitude - p2.latitude)
    
    if denominator < 0 {
      ua = -ua
      ub = -ub
      denominator = -denominator
    }
    
    if ua >= 0.0 && ua <= denominator &&
        ub >= 0.0 && ub <= denominator &&
        denominator != 0 {
      return CLLocationCoordinate2D(
        latitude: p0.latitude + ua / denominator * (p1.latitude - p0.latitude),
        longitude: p0.longitude + ua / denominator * (p1.longitude - p0.longitude
        )
      )
    }
    
    return nil
  }

The result of such cheking is in the next demo:

demo



left - after; right - before

Resources