Know your tools
swift SwiftUI algorithms Dijkstra iOS macOS Estimated reading time: 14 minutesI like to solve some interesting task - the one of the last one has no practical use, but instead just allows me to remind some algorithms and steps for solving problems.
Toolset is very important - u can be a master within some tools, but u may never do some stuff without a proper tool. One of them - an algorithm. There are a lot of articles, books, and other stuff that can describe them.
Articles in this series:
- Know your tools
- Know your tools - part 2
The Problem
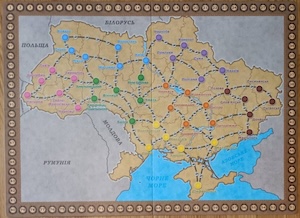
Some time ago, I bought a little card game for my kids. The idea is to travel across the country and visit all the cities on the cards you have.
U may travel by bus or train. In the case of a bus, if you have a few steps in between cities (depending on the city), you can use 1D6 for determining the available step count per turn or use a train. With a train, you need to check the departure board to check available paths, and if there are any, you can perform such a trip in one step.
Solution
Well, to solve this task, I divided it into a few subtasks:
prepare the correct input data.
- select algorithms for search
- visualize the result
Let’s review each of these subtasks.
Prepare the correct input data.
We need to represent all game parts as input for the game solving engine. To do so, we can start with the smallest part - city, after - prepare a set of predefined cities. One more step is to prepare a route map.
A City may be just a simple structure that holds a name and region for us:
struct City: Hashable {
enum Region: Hashable {
case blue
case brown
...
}
let region: City.Region
let name: String
}Thus, we have a lot of cities involved in the game; we need to predefine them so we can operate them during the game.
extension City {
static let lviv: City = .init(region: .pink, name: "Львів")
static let uzhgorod: City = .init(region: .pink, name: "Ужгород")
static let drohobuch: City = .init(region: .pink, name: "Дрогобич")
...
// for each of 7 regions, we need to define 7 cities.And the last part for input data is to determine traveler movement type (car or train).
enum MoveAroundUkraine {
case train
case carand maybe some limitations in rules, such as availableTrainTickets:
enum Rules {
static let availableTrainTickets = 4
}
}Huh, the first step was the easy-one.
Select algorithms for search
Rules recap
According to the rules, we can use 4 tickets to train (1 ticket == 1 move) and unlimited steps for car movement type (1D6 roll as step count or 1 city visit == 1 move). At the beginning of the game, each user receives seven cities one from each region. We can start in any city from 7 on and move in any direction. Before the game starts, each user has time to think and select a route. You may change the route during the game.
Thinking a bit about these rules, we can define a few steps for determining a route for trip:
- Check departure board for available cities and destination - if there is some city within 1-2 tickets, memo them, that’s may be a good variant for the start or maybe for some move.
- Check neighboring regions and cities that you need to visit - if some of them are close to each other to visit them by car - note them.
- Try to model all the available routes and compare them to be able to select the fastest.
This step allow u to select some not bad route. Thus it works, we can do same, but delegating the hard work to computer :].
Algorithm
Looking at this game model, we can see that we have cities connected to other cities - that looks like as a graph, and we also have different steps count between them weighted graph.
The good moment here is that if you have a lot of tools in your bag, you now see a possible way of solving the problem. I like to read a lot and store shortcuts for different options and mechanisms that can be useful in some cases. Algorithms - one such shortcut. Getting all together, we can easily select Dijkstras algorithm for searching a path between weighted components of the graph.
Of course, this is not the full solution. We can see that for train connections, they are directed, and for car - undirected. We also know that we have not 2 cities but 7; this requires us to check and calculate the paths for many routes (7!+).
According to the game-solving algorithm for a normal game (above), we can think of how to convert it and use it in the app. I determine the next steps:
- Separate processes for train and car movement at first; thus, each problem has a different solution complexity, and dividing it will simplify the overall task complexity.
- Determine all train connections; thus, trains connections are not bidirectional; we need to mix them all together and review each pair result.
- Select the best matches for train-based moves based on steps, but no more than 4 steps in total, because according to game rules, each user has only 4 tickets.
- Build a mixed set with selected train moves and all the car movements to allow the next, final fastest path search and reduce the total number of options to check. The result will be a graph with both directed and undirected connections.
- Build a set of possible city combinations: 7! = 5,040 options… because we have 7 cities, and in theory we can mix all cities in order to visit them, thus providing different results in total trip length. We need to check them all. Even if there is an undirected connection, exchanging the positions of two cities in a set of seven, if it does not affect the length of the trip in between those two cities, will affect the total length of the trip for other cities.
- Search for each set from point 5 and calculate the total length of the trip for the selected set.
- Compare and find the minimum value for an array of results
- Store and visualize it.
Huh, at first glance, this was a simple task, but now this task has been transformed a bit. I see at least 4 major subtasks to solve here:
- select available pairs of cities for a train-based move
- calculate the shortest path for two cities in a set
- calculate the shortest set by appending all from the previous step.
- select the shortest path for travel between cities in each set.
We could also could add step for excluding an input city from a set of cities that needs to lookup if the path between already existing cities includes that city (this means that we will travel twice through the city if we do not exclude it). But this is more related to the optimization of the whole process.
if we transform this into algorithmic usage:
- Dijkstra’s algorithm
- Dijkstra’s algorithm
- transform
- min/max search in unordered set
Implementation
I won’t describe the Dijkstra’s algorithm, so there are a lot of tutorials and articles related to it. I used Dijkstra’s algorithm implementation from Swift Algorithm Club.
I recommend reviewing Swift Algorithm Club for more
Before going to implementation, you need to know that I named the type that represents Dijkstra’s algorithm as DijkstraSet.
Every time you u see this name, just know, that it’s a type needed to represent Dijkstra’s algoritm.
Graph.Edge- representsent each edin the in graph,Graph.Vertex- each object,Graph.Visit- represent the place in graph we have checked.
I extend the MoveAroundUkraine enum with a static function, which will do all the magic:
static func dijkstrasSetFor(movement type: Self) -> DijkstraSet<City>
static func calculateFastestTripBetween(_ cities: [City]) -> [Graph.Edge<City>]The first one prepares a set of cities for either a train or a car. The second one - calculate the trip route.
For implementation details, check source code
To implement the algorithm described above, let’s move step by step. So we are starting to determine all train connections suitable for us—connections that require 1-2 steps.
We must prepare a citiesGroupsForTrain set of all possible city combinations by 2, and check trainSet for length by selecting minimal connections, so the total length of which is no more than 4.
During very first implementation, I skip optimizations and other stuff like that; the idea is to get a workable solution and then optimize it.
let citiesGroupsForTrain = cities.permutations(ofCount: 2)
let trainSet = MoveAroundUkraine.dijkstrasSetFor(movement: .train)
var possibleSets: [[Graph.Edge<City>]] = []
for group in citiesGroupsForTrain {
if let vertexFrom = trainSet.adjacencyDict.keys.first(where: { $0.data == group[0]} ),
let vertexTo = trainSet.adjacencyDict.keys.first(where: { $0.data == group[1]} ),
let path = trainSet.dijkstra(from: vertexFrom, to: vertexTo) {
possibleSets.append(path)
}
}
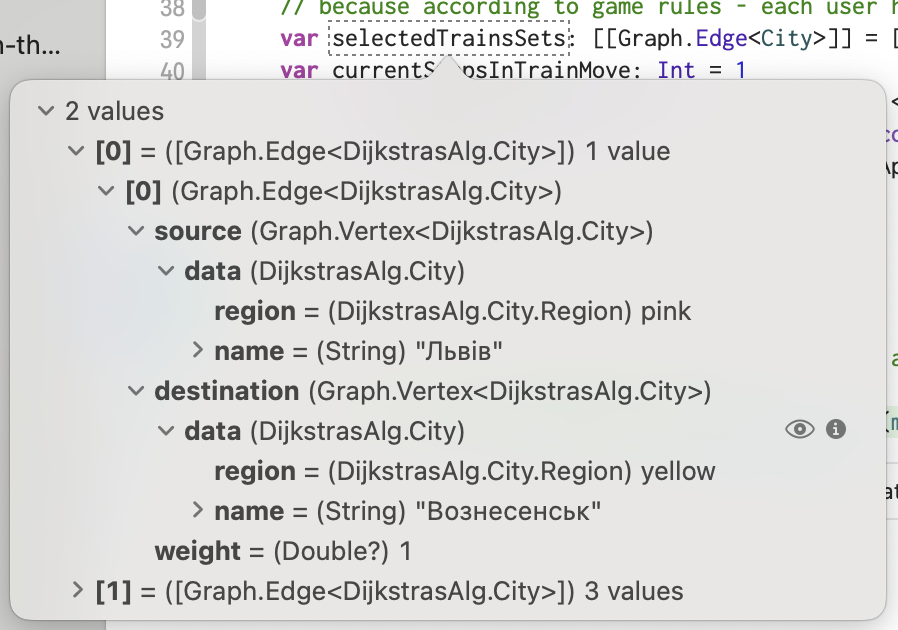
var selectedTrainsSets: [[Graph.Edge<City>]] = []
var currentStepsInTrainMove: Int = 1
while selectedTrainsSets.flatMap({ $0 }).count < MoveAroundUkraine.Rules.availableTrainTickets {
let dataToAppend = possibleSets.filter({ $0.count == currentStepsInTrainMove })
selectedTrainsSets.append(contentsOf: dataToAppend)
currentStepsInTrainMove += 1
}
permutations(ofCount:)available from another SP Apple Swift algorithms
The result of this is a few paths from trains with 1 or 2 or 3 tickets needed, but no more than 4. Anyway this moves is much faster than with a car.
All tests are done with the next set of cities:
let cities: [City] = [
.lviv,
.lutsk,
.cherkasu,
.vinnutsya,
.poltava,
.voznesensk,
.lozova
]Now let’s mix up all car routes with selected train routes. To do so, we just need to add a few edges to the default car set:
let carSet = MoveAroundUkraine.dijkstrasSetFor(movement: .car)
for trains in selectedTrainsSets {
trains.forEach {
carSet.add(.directed, edge: $0)
}
}For now, we have everything we need. The last few steps - just calculate paths via the Dijkstra algorithm and determine which path is the shortest one.
Unfortunately, these operations are expensive because we need to iterate and calculate; you can’t find the smallest value in an unordered array of values without checking all the values. Let’s check what we can get:
All our movements can be described as follows:
let possibleMovements = Array(cities.permutations(ofCount: cities.count)).lazyWe must wrap result of permutation in Array because of COW principles and we can make it lazy, to optimize a bit iterations
We also can combine 2 iterations - one for calculating path and another for searching min value.
The initial result is next:
let possibleMovements = Array(cities.permutations(ofCount: cities.count)).lazy
var bestPathLength: Int = 0
var bestPath: [Graph.Edge<City>] = []
let clock = ContinuousClock()
let interval = clock.measure {
for combIndx in 0..<possibleMovements.count {
let orderedMovementSet = possibleMovements[combIndx]
var currentPath: [Graph.Edge<City>] = []
for idx in 0...orderedMovementSet.count-2 {
let first = orderedMovementSet[idx]
let second = orderedMovementSet[idx+1]
if let vertexFrom = trainSet.adjacencyDict.keys.first(where: { $0.data == first } ),
let vertexTo = trainSet.adjacencyDict.keys.first(where: { $0.data == second } ),
let path = carSet.dijkstra(from: vertexFrom, to: vertexTo) {
currentPath.append(contentsOf: path)
}
}
let length = currentPath.reduce(0, { $0 + ($1.weight ?? 0) })
if bestPathLength > Int(length) || bestPathLength == 0 {
bestPathLength = Int(length)
bestPath = currentPath
}
}
}
print(interval)
print("Best required \(bestPathLength) steps")
for edge in bestPath {
print("\(edge.source) -> \(edge.destination)")
}The result is next:
43.178715084000004 seconds
Best required 29 steps
Луцьк -> Львів
Львів -> Вознесенськ
Вознесенськ -> Балта
Балта -> Вінниця
Вінниця -> Умань
Умань -> Черкаси
Черкаси -> Кременчук
Кременчук -> Полтава
Полтава -> Харків
Харків -> ЛозоваImprovements
Good! calculation is correct, but look at the time needed - 43 sec - a bit too much as for me there are a few more points for improvements:
- searching the vertex is a bit over - we can use preheated values for that
let vertexes = cities.compactMap { city in
trainSet.adjacencyDict.keys.first(where: { $0.data == city } )
}- we can use early exit for path that not finished yet but already has a bigger steps count
loop: for idx in 0...orderedMovementSet.count-2 {
...
if bestPathLength != 0 {
let currentPathLenght = currentPath.reduce(0, { $0 + ($1.weight ?? 0) })
if Int(currentPathLenght) > bestPathLength {
break loop
}
}Re-run the algorithm and see the result. I got next:
27.43803925 secondsBetter.. but still not good… If you check the CPU, it works for about 100% all the time. 1 CPU.. but we have …how many?
ProcessInfo.processInfo.activeProcessorCountOn my MacBook, it’s equal to 6. So in theory, if we could use all of them, we should receive a huge boost.
To do so, we can use concurrentPerform(iterations:execute:), but this is a bit old approach.
If u check new Concurrency framework, we can find the withTaskGroup(of:returning:body:) function. Let’s reimplement the whole algorithm using this function and see the result.
First, let’s make the function async:
static func calculateFastestTripBetween(_ cities: [City]) async -> [Graph.Edge<City>]Then, we can get the count of cores and create groups with tasks to calculate evenly distributed calculations for each of them.
The implementation may include the following:
let valueSet = carSet
let processors = ProcessInfo.processInfo.activeProcessorCount
let progress = Progress(totalUnitCount: Int64(possibleMovements.count))
let task = Task {
let concurrentResults: [Graph.Edge<City>] = await withTaskGroup(
of: ([Graph.Edge<City>], Int).self
) {
group in
for i in 0..<Int(processors) {
group.addTask {
let lowerBound = Float(i)/Float(processors) * Float(possibleMovements.count)
let upperBound = Float(i+1)/Float(processors) * Float(possibleMovements.count)
let data = Array(possibleMovements[Int(lowerBound)..<Int(upperBound)])
var bestPathLength: Int = .max
var bestPath: [Graph.Edge<City>] = []
for combIndx in 0..<data.count {
let orderedMovementSet = data[combIndx]
var currentPath: [Graph.Edge<City>] = []
loop: for idx in 0...orderedMovementSet.count-2 {
let first = orderedMovementSet[idx]
let second = orderedMovementSet[idx+1]
if let vertexFrom = vertexes.first(where: { $0.data == first }),
let vertexTo = vertexes.first(where: { $0.data == second }),
let path = valueSet.dijkstra(from: vertexFrom, to: vertexTo) {
currentPath.append(contentsOf: path)
let currentPathLenght = currentPath.reduce(0, { $0 + ($1.weight ?? 0) })
if Int(currentPathLenght) > bestPathLength {
break loop
}
}
}
let length = currentPath.reduce(0, { $0 + ($1.weight ?? 0) })
if bestPathLength > Int(length) {
bestPathLength = Int(length)
bestPath = currentPath
}
progress.completedUnitCount += 1
print(progress.fractionCompleted )
}
return (bestPath, bestPathLength)
}
}
var bestPathLength: Int = 0
var bestPath: [Graph.Edge<City>] = []
let clock = ContinuousClock()
let interval = await clock.measure {
for await value in group {
let length = value.1
if bestPathLength > Int(length) || bestPathLength == 0 {
bestPathLength = Int(length)
bestPath = value.0
}
}
}
print(interval)
return bestPath
}
return concurrentResults
}After the first test, I got this result:
10.222808 secondsThat’s almost twice as good as before. Can we improve even more? I guess yes.
- skip cities in the path for checking if the discovered path between cities in the set already includes that city.
- cache city-to-city path calculation (because 7 variants has a lot of similar paths, but we re-calculate them every time)
- skip options with a city-to-city path that is too long
- other options?
I won’t dive into these improvements more (at least for now) - 10 seconds is good enough for testing purposes. The most interesting part of this trip I have covered; all others can be improved infinitely.
visualize result
This part will be covered in the next article.
Conclusion
Wow. That was a huge section. We have a not-bad algorithm that can solve the task; we can get a result that can already be used. But would it be nice if we could visualize the search process on a map?
Resources
Share on: